

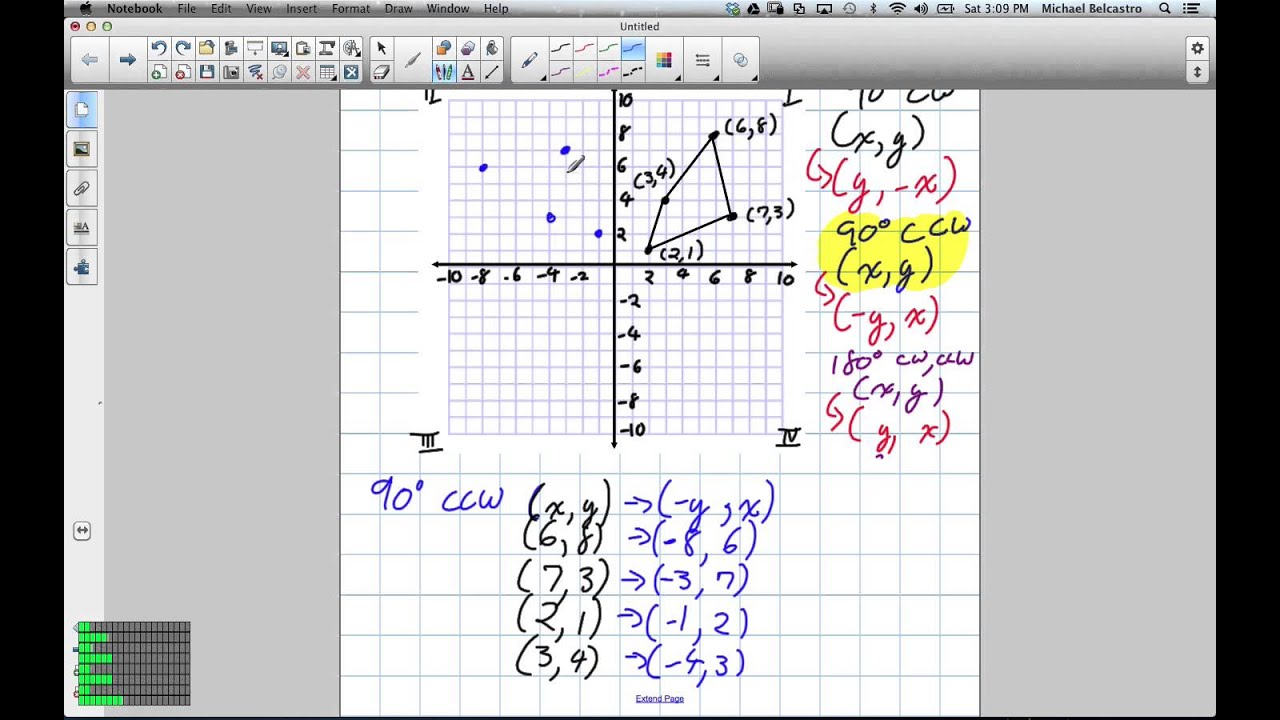
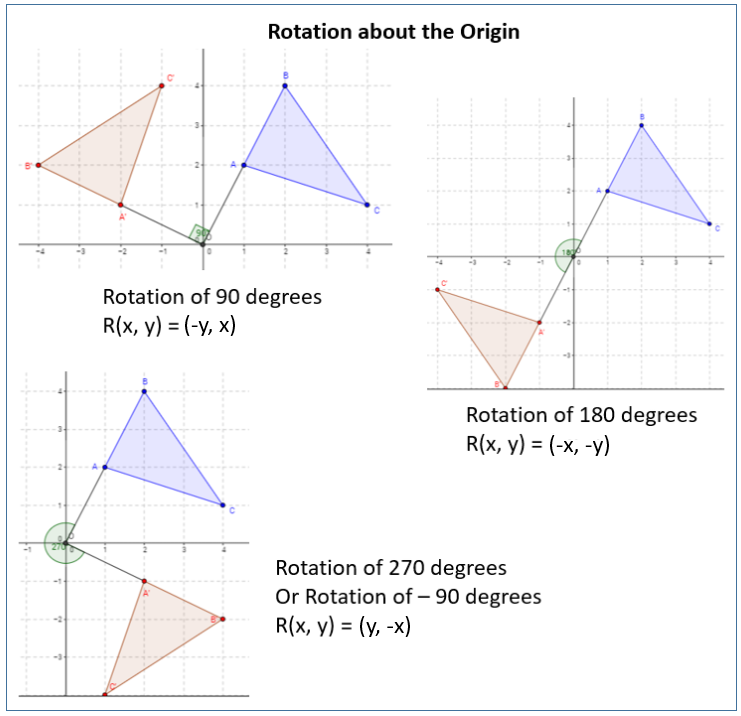
You can use this rule to rotate a pre-image by taking the points of each vertex, translating them according to the rule, and drawing the image. How do you calculate a 90 degree rotation? The general rule for rotation of an object 90 degrees is (x, y) -–> (-y, x). Let’s understand the rotation of 90 degrees clockwise about a point visually. What is a 90 degree rotation clockwise?Īnswer: To rotate the figure 90 degrees clockwise about a point, every point(x,y) will rotate to (y, -x). How do you rotate a point 90 degrees clockwise?Īnswer: To rotate the figure 90 degrees clockwise about a point, every point(x,y) will rotate to (y, -x). In other words, switch x and y and make y negative. This means, we switch x and y and make x negative.ĩ0 Degree Rotation When rotating a point 90 degrees counterclockwise about the origin our point A(x,y) becomes A'(-y,x). What is 270 degrees rotated?Ģ70 Degree Rotation When rotating a point 270 degrees counterclockwise about the origin our point A(x,y) becomes A'(y,-x).
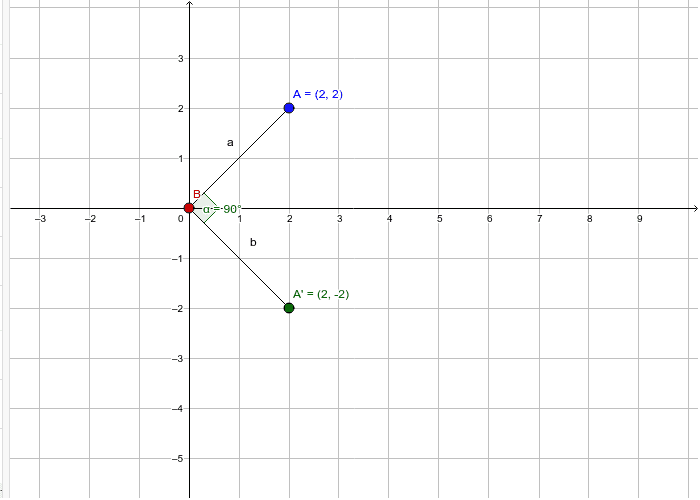
If you plug in 5 and 66.87 for r and θ, you find that the rotated point (x1,y1) = (1.964, 4.598). The x coordinate of the rotated point is rcos(θ), and the y coordinate is rsin(θ). How do you find the coordinates of the image of a point after a 270 degree rotation?Īnswer – To find the coordinates of point (x,y) after a 270° counterclockwise rotation about the origin, multiply the x-coordinate by -1 and then interchange the x- and y-coordinates. What is the image of point 3/5 If the rotation is?Īnswer: The image point will be (-3, -5). The rule for a rotation by 90° about the origin is (x,y)→(−y,x). How do you calculate a 90 degree rotation? Therefore, the new position of point M (-2, 3) will become M’ (3, 2). When the point is rotated through 90° clockwise about the origin, the point M (h, k) takes the image M’ (k, -h). What are the coordinates of the image after a rotation of 90 clockwise?
Next for Q 1 1, print the element at row index 1 and column index 1 of A, which is 6. R 90 and R 90 => 90 + 90 => 180 degrees in clockwise direction).Īfter rotation the matrix will now become So the updated matrix will be,Īfter updating, we need to rotate the matrix by sum of all rotation angles applied till now(i.e.
90 CLOCKWISE ROTATION UPDATE
1 will represent the end of input.Outputįor each Query operation print the element present at row index K and colum index L of the matrix in its current state.Explanationįor R 90, clockwise rotation by 90 degrees, the matrix will becomeįor Q 0 0, print the element at row index 0 and column index 0 of A, which is 3.įor Q 0 1, print the element at row index 0 and column index 1 of A, which is 1.Īgain for R 90, clockwise rotation by 90 degrees, the matrix will becomeįor Q 0 0, print the element at row index 0 and column index 0 of A, which is 4.įor U 0 0 6, update the value at row index 0 and column index 1 in the initial matrix to 6. Each operation on each line (Beginning either with R, U or Q). Next lines contain various operations on the array. Next N lines contain N space-separated integers Aij (i - index of the row, j - index of the column). The first line contains a single integer N. You need to print the value at row index K and column index L of the matrix A. In initial matrix A (as given in input), you need to update the element at row index X and column index Y with value Z.Īfter the update, all the previous rotation operations have to be applied to the updated initial matrix.
The angle of rotation(S) will always be in multiples of 90 degrees. You need to rotate the matrix A by angle S in the clockwise direction. Rotation: It is represented as R S where S is an integer in which denotes the number of degrees to rotate. You need to apply the below given 3 operations on the matrix A. You are given a square matrix A of dimensions NxN.


 0 kommentar(er)
0 kommentar(er)
